Il paradosso del compleanno

Qualche giorno fa mi era venuta in mente la seguente domanda:

Quante persone devono esserci in una stanza affinché ci sia almeno il 50% di possibilità che almeno 2 di loro siano nati lo stesso giorno dell’anno? (ad. es. il 1° gennaio).

La certezza dell’evento (ossia la probabilità che l’evento si verifichi è =1) è SOLO quando sono presenti 367 persone (nel caso di anni bisestili): una per ogni giorno dell’anno bisestile, + un’altra persona che PER FORZA è nata in un giorno già “occupato” da qualcun altro.

Quindi ho pensato: se la certezza è 367, per avere il 50% di possibilità di riuscita dovranno essere circa la metà di 367, ovvero 183-184 persone. Ma siccome spesso il calcolo combinatorio ci rivela cose che non ci aspettavamo, avevo concesso alla mia “intuizione matematica” un margine di errore, arrivando a supporre che anche con solo un centinaio di persone la probabilità fosse circa del 50%.

Allora ho cominciato facendo i conti ma arrivavo a conclusioni completamente sballate (già con una ventina di persone arrivavo al 60% di possibilità di riuscita): allora ho contattato @Pazqo e gli ho sottoposto il mio quesito.

Lui mi risponde in men che non si dica, dicendo che già con una ventina di persone la possibilità è circa del 50%. COSACOSACOSA?? O_o
Allora avevo ragione? Ovviamente no, in matematica se ci si sbaglia di un 10% ci si sta sbagliando e basta. :)

Però, siccome anche la soluzione giusta andava a sfracellarsi contro gli scogli della mia intuizione, ho chiesto maggiori dettagli e Pazqo mi risponde che questo problema è noto come “Paradosso del compleanno” (qui mi sia permesso un appunto: la parola “paradosso” non va intesa propriamente in senso logico-matematico, ovvero che a partire da premesse vere si arriva a conclusioni contraddittorie, ma va intensa in “senso comune”: è un paradosso nel senso che si scontra col nostro intuito).

Su wiki c’è già tutto, ma mi sono flashato talmente tanto che vi riassumo come si imposta il problema: l’idea è che per calcolare in maniera diretta la probabilità che l’evento si verifichi occorre fare una marea di calcoli che, ad ogni nuova aggiunta, eliminino le singole probabilità che le persone che ho già contato non siano nate lo stesso giorno dell’ultima persona introdotta (“principio di inclusione-esclusione”).

Pazqo mi dice che il modo più semplice per effettuare il calcolo è quello di calcolare la probabilità complementare, ovvero la probabilità che, ad ogni nuova persona aggiunta, NON si dia il caso che essa sia nata lo stesso giorno di quelle già considerate.

Tale probabilità si calcola così:

– Detto P(2) la probabilità che 2 persone NON siano nate lo stesso giorno, essa è evidentemente: (casi favorevoli / casi possibili) = 365 / 366.

Detta P(3) la probabilità che 2 persone NON siano nate lo stesso giorno, essa è evidentemente: 364 / 366

e via dicendo…

Ora noi vogliamo che TUTTE queste possibilità si verifichino contemporaneamente, ovvero, tradotto in matematica, dobbiamo fare un prodotto con tutte le frazioni che otteniamo.

P(totale) sarà quindi: P(2)*P(3)*P(4)*…

A noi però interessa l’evento completare, no? Perché questa è la probabilità che N persone NON siano nate lo stesso giorno. Quindi facciamo il calcolo e poi sottraiamo dalla certezza il nostro risultato: 1 – P(totale)

Questo è quello che otteniamo, mano a mano che aggiungiamo persone, è:

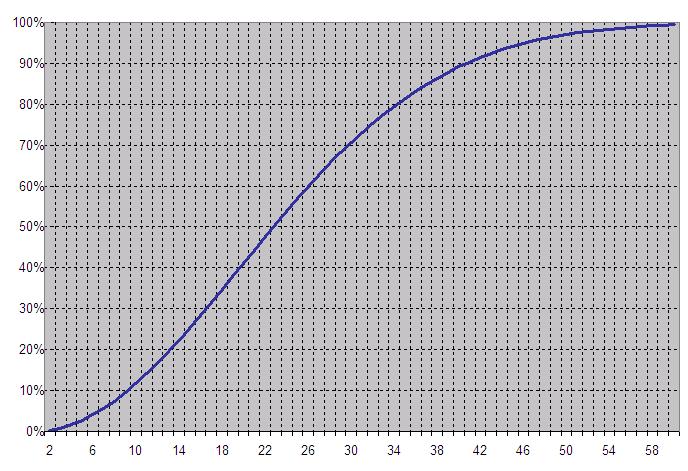
Come vedete, la certezza si ha asintoticamente proprio con 367 persone, come avevamo supposto all’inizio (qui non riporto il grafico oltre le 60 persone perché altrimenti veniva troppo piccolo), ma già con 23 la possibilità di vittoria è del 50% (molte meno delle 100 che avevo ipotizzato!!), mentre con 60 persone aumenta fino ad un drastico 99% !!! O_O

Cazzo ancora mi ci devo abituare a questo risultato, però poi penso alla frase EPICA di John Von Neumann e mi tranquillizzo: ”La matematica non si capisce, alla matematica ci si abitua” (considerando che è stato uno dei matematici più brillanti di sempre..)

Quindi, se siete in un ristorante mediamente affollato e non avete il portafogli (ma non vi va di fare la figura dei pezzenti) scommettete con un vostro commensale che nel ristorante ci sono almeno due persone nate lo stesso giorno. Siccome è un fatto controintuitivo quello scommetterà e voi vi farete pagare la cena! :res:

Approfondimenti:
wiki
Richard von Mises, lo scopritore di tale paradosso.