Controlli Dinamici
Dopo aver visto lo stupore che ha provocato la visione di un pendolo inverso vediamo
se riesco a spiegare un po’ di cose inerenti a questo tipo di problemi e nello specifico cosa sia il controllo di un sistema dinamico.
Qualche Esempio:
Per capire subito cosa si intende per controllo di un sistema pensiamo di essere in autostrada e di voler fare i bravi mantenendo una veloctà costante di 130 km/h.Ovviamente siamo con una Ritmo Cabrio e non c’è il controllo automatico di velocità.
Quindi cosa facciamo? I nostri occhi guardano il tachimetro, il nostro cervello elabora se la velocità istantanea è maggiore o minore di quella richiesta (set point) e tramite il piede solleviamo o schiacciamo il pedale del gas.
Oppure pensiamo al termostato di casa: impostiamo una temperatura, un termometro la rileva e a seconda di questa attua una determinata politica di funzionamento.
Anche il sistema di controllo del pendolo inverso può funzionare cosi! Ci sono dei sensori nel fulcro del pendolo che ne indicano l’angolo e il sistema evolverà in modo da portare, e mantenere, il pendolo nella posizione desiderata (cioè nella posizione opposta alla partenza)
Loop di Controllo:
Tutti questi esempi hanno in comune una cosa, un loop di controllo, cioè un sistema che controlla l’uscita istantanea (nei nostri casi: occhio, termometro, sensori) e che tramite degli attuatori (piede,accensione/spegnimento termosifoni, movimento del carrello) andrà a modificare lo stato del sistema, cercando di portarlo più vicino al set point (130 km/h, temperatura impostata, posizione desiderata del pendolo) fino al raggiungimento di questo.Modellizzazione:
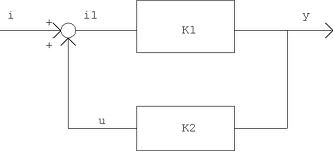
Quei rettangoli rappresentano, nello schema a blocchi, il nostro sistema da controllare (K1) e il controllore stesso (K2) mentre i e y sono entrate e uscite. Il cerchio con i due più a sinistra indica come l’ingresso e il segnale di controllo (u) entrano nel sistema in esame, mentre l’incrocio a valle del sistema rappresenta l’acquisizione dei dati mediante sensori. Ma come dare un descrizione rapida e funzionale del tutto? Ovviamente passando per un po’ di sana matematica.
Tralasciando un po’ la modellizzazione del controllore vediamo soltanto quella del sistema da controllare che è più interessante. Dobbiamo scrivere un po’ di equazioni che a fronte di un particolare ingresso danno in uscita grossomodo quello che fa o quello che produrrebbe il sistema reale a fronte dello stesso ingresso
(se dò un calcio al pallone, il modello del pallone mi deve dire che questo assumerà velocità tot e magari non si mette a oscillare tipo ufo in aria!).
Per quanto riguarda la modellizzazione del sistema di controllo il ragionamento è inverso, cioè partiamo dal modello del controllo e poi vediamo se messo nel sistema reale funziona.
Equazioni Differenziali:
Le equazioni di cui parlavo prima sono un po’ particolari, sono generalmente equazioni differenziali, cioè equazioni in cui l’incognita non è un valore ma una funzione, che soddisfa una serie di relazioni con le sue derivate (ad esempio $latex y’ = y$, in cui $latex y = y(t)$ è una funzione reale, ha per soluzione la funzione esponenziale ($latex y(t) = e^t$) perché l’esponenziale è l’unica funzione che coincide con la sua derivata: infatti $latex (e^t)’ = e^t$. Questo è l’esempio più semplice di equazione differenziale).Da un punto di vista più fisico quando deriviamo rispetto al tempo l’equazione di descrive come varia la crescita di una funzione rispetto al tempo.
Ad esempio, la derivata della posizione è la velocià e la derivata di quest’ultima è l’accelerazione.Che scritto in modo più elegante:
$latex v=\frac{dx}{dt}$ ; $latex a=\frac{dv}{dt}$
indicando con v la velocità, x la posizione e a l’accelerazione. Le frazioni che vedete sono un altro modo per indicare le derivate di una funzione rispetto a una funzione (in questo caso il tempo).
Si leggono appunto:
– La velocità è la derivata della posizione rispetto al tempo
– L’accelerazione è la derivata della velocità rispetto al tempo
Modello del Pendolo
Adesso che sappiamo almeno un po’ di cosa si parla andiamo ad analizzare il problema del pendolo.
Prima di passare al modello nudo e crudo vorrei spendere due parole sulla fisica del pendolo rigido. Esso ha due punti di equilibrio (la verticale in basso e la verticale in alto). Pur essendo entrambi punti di equilibrio, il primo è stabile o attrattivo (se diamo un colpo al pendolo esso infatti oscillerà nel suo intorno) mentre l’altro è instabile (se diamo un colpo al pendolo in questa posizione, comincia a oscillare senza più possibilità di ritorno, oscillando appunto intorno al punto stabile). Perché il pendolo tende ad assumere la posizione verso il basso? Perché è quella con energia potenziale minore! L’energia potenziale di un oggetto è direttamente legata all’altitudine a cui si trova rispetto a un dato sistema di riferimento. Una volta assunta questa configurazione, se non agiscono forze esterne, è pressoché impossibile che ritorni ad assumere (staticamente) la posizione che aveva nel punto di eq. instabile! E qui entreremo in gioco noi che con il nostro carrellino forniremo energia al sistema!
Ma vediamo un grafico che spiega meglio quello che ho detto a parole:

Questo è un diagramma di fase di un pendolo, cioè un grafico che ci dice cosà farà il nostro pendolo in funzione dell’energia fornita. Le curve, che rappresentano i livelli di energia, ci descrivono varie situazioni a seconda della geometria: quelle concentriche indicano che il nostro pendolo sta oscillando intorno al punto di eq. stabile mentre le curve aperte indicano che il nostro pendolo sta effettuando rotazioni complete in un verso. Come vediamo le due zone sono separate da una linea rossa ed è proprio questo il nostro “obiettivo energetico”. Le due linee rosse vanno a incontrarsi proprio sul punto che abbiamo chiamato instabile, mentre l’origine delle curve chiuse, al centro, è il nostro punto stabile. Noi, con il carrello, dovremo mantenere il più possibile l’energia del sistema vicino alla linea rossa. Notiamo che questa è la situazione “senza attrito”, in cui l’energia si conserva. Nel caso con attrito, che è quello reale, il sistema si complica un po’, ma non è così importante.
Modello del pendolo inverso
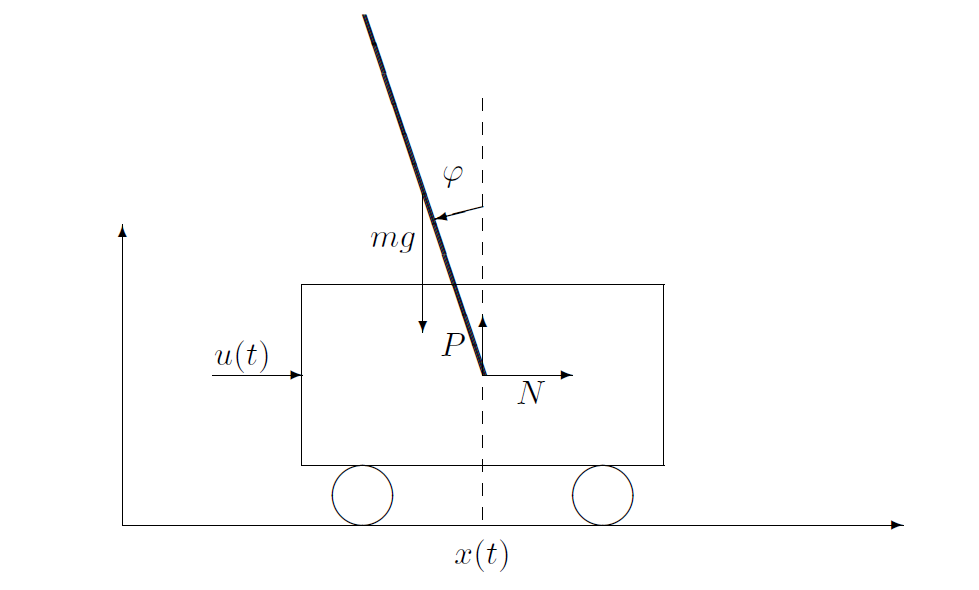
Qui siamo di fronte a un sistema complesso da modellizzare perché ci sono 2 corpi in movimento.
Intanto descriviamo le forze che agiscono sul centro di massa del pendolo (e quindi velocità e posizione) in termini delle componenti orizzontali e verticali.
1. $latex N(t)=m\frac{d^2}{dt^2}(x(t)-L \sin\varphi(t))$
2. $latex P(t)-mg=m\frac{d^2}{dt^2}L \cos\varphi(t)$
Usiamo queste due per comporre il moto rotativo del centro di massa del pendolo:
3. $latex I \frac{d^2\varphi(t)}{dt^2}=LP(t) \sin \varphi(t) + LN(t) \cos\varphi(t)$
Mentre per il moto del carrello abbiamo:
4. $latex M \frac{d^2 x(t)}{dt^2}= -N(t) + u(t) – b \frac{dx(t)}{dt}$
Vediamo di dare un senso a questa cascata di lettere che ho scritto:
1. Qui siamo di fronte, anche se in modo un po’ criptico, alla famosa $latex F=ma$, l’equazione di Newton che descrive la forza come una massa per una accelerazione. Qui esprimiamo la componente orizzontale della velocità del centro di massa del pendolo. L è la distanza che c’è tra il fulcro e il centro di massa del pendolo mentre $latex \varphi(t) $ è l’angolo che si crea tra pendolo e la verticale ideale. E’ in funzione di t in quanto ci si aspetti vari durante l’esperimento, anzi sarà proprio lui l’oggetto del nostro controllo. m è la massa del pendolo.
2. Idem con patate solo nella componenten verticale.
3. Adesso che sappiamo le forze che agiscono sul centro di massa possiamo “fondere” le 2 equazioni precedenti in un unica equazione che dice come tutto il sistema pendolo ruota. Quindi sto passando da moti rettilinei a moti rotativi, che mi descrivono meglio la dinamica del sistema. I è il momento di inerzia del pendolo.
4. Questa equazione è del tipo di 1. e 2. ma è riferita al carrello con massa M. Dobbiamo però focalizzare la nostra attenzione su u(t): questa forza sarà quella su cui dovremo contare per mantenere il nostro pendolo in verticale, cioè sarà la nostra variabile di controllo. A contorno della cosa ho inserito un attrito viscoso (cioè che diventa tanto più resistente quanto più veloce andate) che si oppone al moto.
Adesso ci possiamo occupare della forma del controllore. Senza perdita di generalità possiamo considerare il controllore realizzato in modo proporzionale cioè esso eserciterà una azione di controllo, mediante u(t) quindi lo spostamento del carrello, proporzionale all’errore che c’è tra dove sono e dove voglio arrivare. Quindi, se per esempio sono a 1 grado dalla posizione ottimale, mi sposterò di pochissimo, se invece sono molto distante il mio carrello si sposterà velocemente. Possiamo comunque decidere quanto “potente” debba essere la componente proporzionale del controllore mediante un coefficiente costante chiamato appunto coefficiente di proporzionalità che andrà a regolare l’azione del controllore. Se il coefficiente è troppo piccolo non avrò “cattiveria” necessaria per riportare il pendolo in posizione ottimale quando sono molto lontano dalla posizione predefinita. Se invece è troppo grande avrò un controllo nervoso che alla più piccola deviazione farà corrispondere un ampio movimento del carrello.
Questo è il più semplice tipo di controllo, ma per completare il discorso devo introdurre il controllore PID. Questo tipo di controllore non è solamente proporzionale ma racchiude dentro di se dei contributi che provengono dall’azione integrativa e differenziale: appunto PID = Proporzionale, Integrale, Differenziale. E’ un controllore più completo che migliora determinate caratteristiche del sistema controllato. Poi ci possiamo inventare altri migliaia di tipi di controllori (anche senza sfruttare la retroazione!) ma il PID resta, nelle applicazioni pratiche, la scelta per il 99% dei casi.
Questo era il mio primo articolo spero che vi sia piaciuto!
Devo ringraziare Pazqo che mi ha assistito e s(u/o)pportato nella stesura!
Link:
Controllo Automatico su Wikipedia
Fondamenti di Automatica – Bolzern (PoliMi)



